如何按照差分阻抗规范进行设计

2021-11-25

如何按照差分阻抗规范进行设计

差分阻抗的概念本身是一种数学结构，它不能完全捕捉差分走线中每个信号的行为。差分阻抗是另一个重要值的捷径，奇模阻抗，反之亦然。那么我们需要针对哪些设计以及如何确保信号在接收器处正确解码？

差分阻抗定义

差分阻抗与差分信号的基本特性有关。所有差分信号都由接收器组件解释为差分信号（因此称为“差分”）。考虑差分信号的一种方式是：它是一种传播的电磁干扰，涉及两个不同的信号，理想情况下沿着一对走线一起发送。当我们说“电磁干扰”时，我们指的是两条轨迹周围的电场和磁场分布。毕竟，这就是PCB中导体的全部意义所在：引导和传输布局周围的电磁场。

因此，看看这对信号产生的电磁干扰如何沿两条迹线传播是很有趣的。为此，我们需要：

电磁场所经历的传输线阻抗

这种干扰的传播常数

如果您知道这些值之一，那么您就可以计算出另一个值。设计特定差分阻抗的重点是确保我们注入通道的电磁场被解释为在通道负载端接收到的相同（或几乎相同）的电磁场。

这里应该有趣的是如何使用每个跟踪生成的字段。我的意思是，我们关心两个信号（它们的场）之间的差异，或者它们的总和，这取决于接收器的功能。因此，就 Telegrapher 方程而言，我们想看看这两个信号的差异的传播，这是一个数学要求很高的主题，需要定义迹线之间的互电容和电感。

差分阻抗公式

计算差分阻抗是计算另一个重要量的练习，即奇模阻抗。当两条走线作为差分对布线并用差分信号驱动时，单条走线的阻抗将是奇模阻抗值。

 

不幸的是，对于差分阻抗，或更具体地说，奇模阻抗，没有很多好的分析模型。如果您查看 Brian C. Wadell 的传输线设计手册，您会发现确定一对微带线的阻抗需要使用 70 个公式（参见第 4.5 节）。这不是印刷错误，它确实需要总计计算一对微带线的奇模或偶模阻抗的 70 个公式。如果您想使用共面排列或不对称轨迹，您将需要更少的公式，但您需要计算椭圆积分，这是我从未做过的事情，并且会采用像 MATLAB 或 Mathematica 这样的应用程序。

您可以直接从麦克斯韦方程中获得互感或互电容，尽管这些结果是许多研究论文的主题，而且结果并不总是那么容易使用。它们往往涉及一组具有多个参数的丑陋公式。这就是为什么您会在网上看到如此多的差分阻抗计算器仅使用 IPC-2141A 公式的原因，这些公式是使用较少公式的近似值。

计算宽度和间距

如果您计算出走线达到特征阻抗目标（即50欧姆）所需的宽度，然后将该宽度插入差分阻抗计算器中，您会发现您不会总是得到有用的间距结果; 间距可能太小（<4 密耳）并且可能超出了非常薄的电介质的制造能力。相反，对于较厚的电介质，间距最终可能会非常大。实际上，在2层标准厚度PCB上，在标准核心上，微带达到50欧姆阻抗所需的走线宽度约为 105欧姆。为了使单个迹线具有等于特征阻抗的奇模阻抗，您的场解算器会告诉您需要将迹线分开大量。如果您使用场解算器，您会发现当间距约为10英寸时，它可能会停止收敛！显然，这也没有用。

一般来说，有许多走线间距和宽度组合可以让您达到差分阻抗规格。您真正设计的是奇模阻抗，而不是差分阻抗，差分阻抗只是定义奇模阻抗的规范。那么，我们不禁要问，在没有公式的情况下，我们如何确定奇模阻抗以及客观上的走线宽度和间距组合？

比较差分微带线的宽度和间距

要了解走线宽度和间距的哪种组合会提供所需的差分阻抗，让我们看一些仿真结果。在下面的示例中，我将运行以下过程 

计算差分微带线对中特定走线宽度所需的走线间距，目标是达到 100 欧姆的目标差分阻抗。

扫描多个电介质厚度值（到微带参考平面的距离）。

对于每个电介质厚度值，请注意 50 欧姆特性阻抗所需的走线宽度。

我将在 Altium Designer 中使用层堆栈管理器执行这些操作，以便用户可以复制它们。在下图中，我展示了不同走线宽度和电介质厚度的差分微带线所需的一组间距值（下面标记为 H，针对 100 欧姆差分阻抗目标和 Dk = 4.8 绘制，不考虑色散或粗糙度）。这里的想法是确定给定宽度所需的间距，目标是达到特定的差分阻抗值。

 

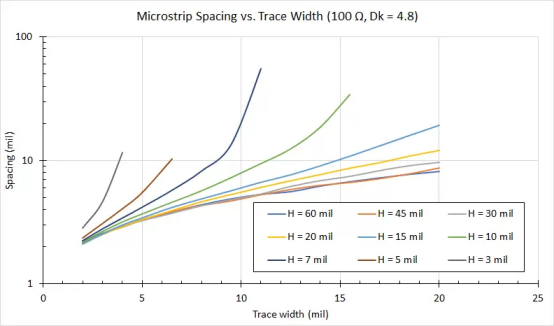
图 1. 间距和宽度值对将在不同厚度的 Dk = 4.8基板上提供100欧姆的差分阻抗。

请注意，为清楚起见，y 轴采用对数刻度。我们可以为其他Dk值和差分阻抗值生成一组新曲线。这些曲线应该说明电介质厚度的作用；随着微带线与其接地平面的距离增加，达到 100欧姆阻抗所需的宽度与间距比对接地距离的依赖程度降低（参见60密耳和45密耳阻抗曲线）。

上面显示的宽度值与50欧姆特性阻抗所需的值相比如何？下图显示了这些值。这是一个很好的线性模型，它说明了在较宽的走线宽度处发生的饱和；当轨迹很宽时，宽厚比变得恒定。

 

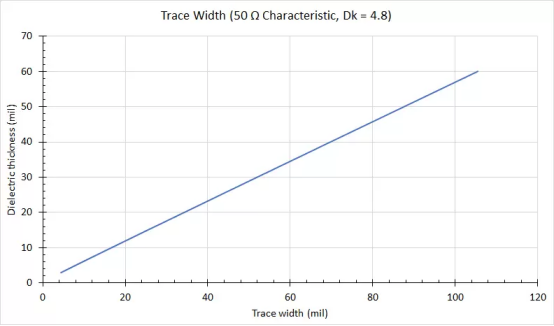
图 2. Dk = 4.8衬底上特性阻抗为50欧姆时的电介质厚度与走线宽度的关系。

现在根据上面显示的特征阻抗和走线宽度/间距对的值，我们可以确定导致50欧姆奇模阻抗的走线宽度也产生50欧姆特征阻抗的间距。

 

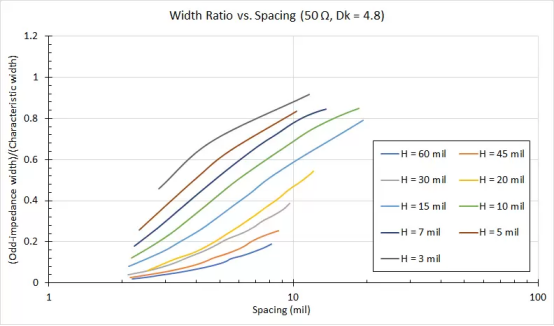
图 3. 不同厚度的 Dk = 4.8基板上100欧姆差分阻抗的间距和宽度比对。

这个图可能看起来很复杂，但它有一个简单的解释。每条曲线在 y 轴上与 1 相交的间距值将导致差分对中的走线宽度等于走线不是差分对的一部分时的走线宽度，同时仍提供相同的阻抗。换句话说，隔离的走线和成对的走线在每个电介质厚度的特定间距值下将具有相同的宽度和50欧姆阻抗。

不幸的是，奇模阻抗和特性阻抗永远不相等。这只会发生在大间距限制中，或者当成对被无限远的距离分开时！y = 1的值是此图上的渐近线。如果电介质很薄（<15密耳），那么对于差分对中给定的走线间距，您将更接近于使走线宽度重合。

举个例子，如果我们采用图3中5密耳的电介质，我们计算奇模阻抗的走线宽度，我们将得到6.184密耳。如果我然后使用它来计算特征阻抗，我会得到55欧姆的值，或者只有 10% 的偏差。这是在某些信号标准中您可以接受的阻抗偏差的高端。例如，USB SuperSpeed 更宽容，允许差分阻抗（因此奇模阻抗）有很大的变化。

使用间距和走线宽度为您带来优势

您可能想知道，具有同时适用于特征阻抗和奇模阻抗的单一走线宽度真的那么重要吗？这有三个很好的理由：

它将设计差分通道的问题从涉及2个变量的问题转换为涉及1个变量：间距。

当您仅设计适用于差分和单端阻抗的单一迹线宽度时，制造商更容易确保受控阻抗。根据您设计中的容差，您可以使用一种宽度来满足单端和差分规格的容差。

您可以在路由差分通道时解耦走线，甚至非常靠近接收器，而且您不必担心反射，因为从接收器看，走线的每一端都将匹配每个端口的输入阻抗.

请注意，这在较薄的电介质上更容易，在厚电介质上，特征迹线宽度和奇模迹线宽度之间的对应关系不会几乎相同。如果您想在使用较厚的电介质时有更多的回旋余地，您还可以选择另一种样式，例如共面差分对。