电流如何加载影响信号

2020-05-18

使用简单的电路和简单的信号源，通常很明显，不同的电路和负载如何影响电路输出端的信号行为。对于更复杂的电路和宽带模拟信号，信号本身如何受到电路本身的影响或电流负载如何影响信号的行为并不总是很明显。尽管您可以手工解决信号行为的这些方面，但并不是每个人都是数学家，并且您将需要一些工具来加快复杂电路的分析速度。

频域还是时域？

在分析信号行为时，选择在频域还是时域工作取决于要从设计中提取哪些信息。如果您使用数字信号驱动电路，则通常不必担心频域中发生的事情，因为信号的功率谱是明确定义的。相反，您应该查看电路中信号的瞬态行为，以确保信号的上升时间在规格范围内。

使用宽带信号或谐波信号时，是否需要在频域或时域中工作取决于您的特定应用。最有可能的是，您将需要确定两种情况下的信号行为。这些类型的仿真的目的是检查输入信号在时域中是否没有过度失真，以及一旦信号到达负载，是否保留了信号的频率内容。

这是处理不同类型信号时要检查的一些重要点。您需要跟踪负载组件上的信号（负载两端的电压或进入负载的电流）。

 

当您将负载添加到现有电路时，负载会耦合回该电路并创建一个新的等效电路。这意味着您不仅可以单独模拟负载组件，还需要将其添加到电路中并模拟整个系统。这是直接在原理图中使用电路仿真工具中的电阻性和电抗性负载轻松实现此目的的方法

。

电流负载如何影响信号：电阻负载和无功负载

由于单个组件无法单独检查各个组件对输入波形的影响，因此我们必须在较大的电路中查看这些组件。下图显示了一个简单的电路，其中的FM源（1 A，1 kHz，调制指数为4）连接到Pi滤波器和电阻负载（R2）。这种类型的信号源具有很强的调制能力，在时域中很容易看出来，但是R2的时间行为并不总是很明显。下面的Pi滤波器用作低通滤波器，但也可以通过互换电容器和电感器将其更改为高通滤波器。

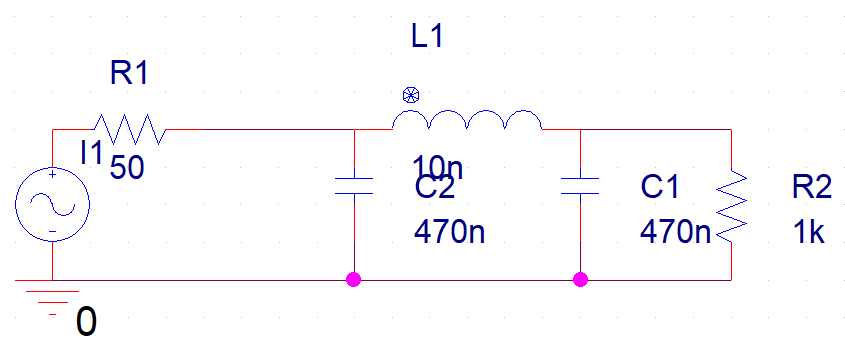
具有50 Ohm输出阻抗的FM源连接到Pi滤波器和下游负载（R2）

由于负载是电阻性的，因此与源波形相比，我们应该期望简单的低通滤波和负载处波形的相移。该滤波器的截止频率为〜2.3 MHz，因此我们不应期望源的载波频率出现严重衰减。但是，源上的电阻输出（R1 = 50 Ohms）将影响瞬态响应，并会改变传递函数。通过查看时域和频域中负载处的波形，可以看到负载和任何上游电路如何改变信号行为。

下图显示了一个简单的瞬态分析，它比较了源电流波形（绿色）和负载电流（红色）。我们可以看到瞬态响应在前约1 ms内消失，并且负载处的波形在以后的所有时间都保持一致。显然，信号电平会有所衰减，但这主要是由于Pi网络和负载的综合阻抗，而不仅仅是负载本身。

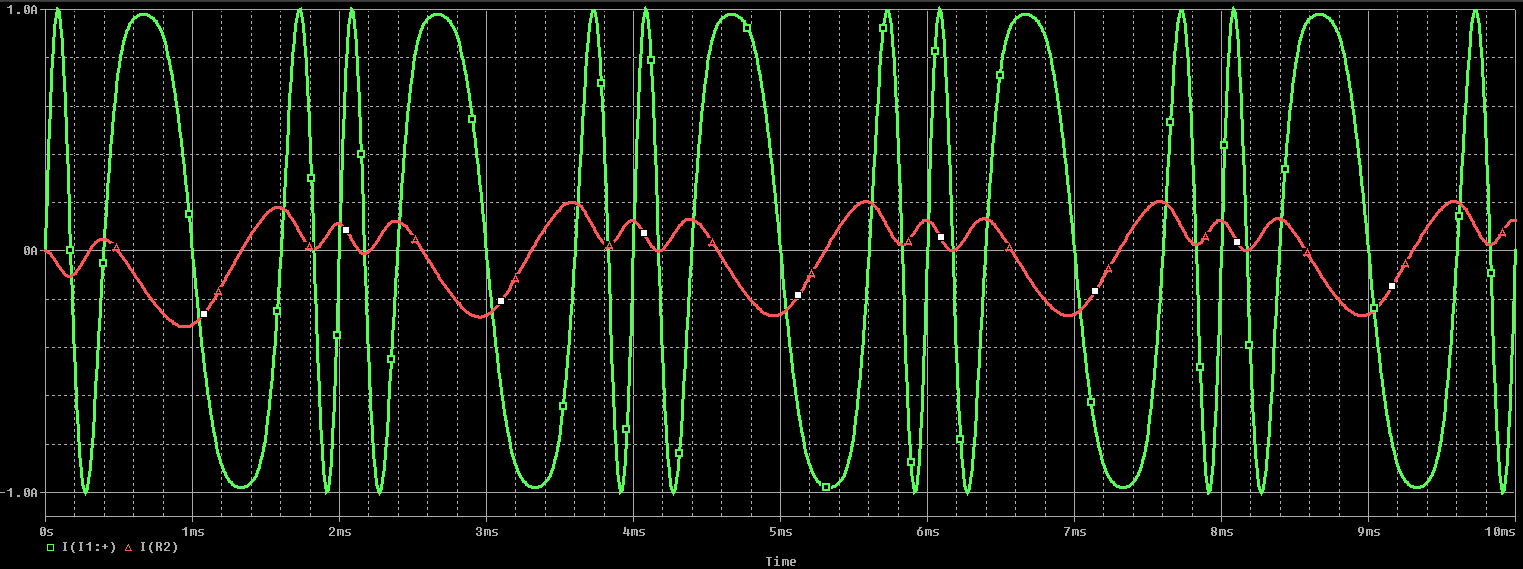
时域中源（绿色）和负载（红色）处的电流波形

在此仿真中要考虑的重要一点是时域中的分辨率。在此，分辨率设置为10μs，即载波频率振荡周期的1％。在上述迹线中，每1 ms周期总共有1000个数据点。在PSpice中，创建模拟配置文件时可以轻松设置这些模拟参数。

连续频域仿真结果

当您想在频域中比较源信号和负载信号时，可以对上述结果进行傅立叶变换。为了真正了解信号中不同频率分量的影响，您应该对负载处的电流波形进行归一化，以使峰值负载电流等于时域中的峰值源电流。下图显示了电路如何在频域中影响FM信号。在红色轨迹中，会出现轻微的滚降，但这不是由于Pi滤波器的传递函数引起的，因为我们正在处理低频信号。

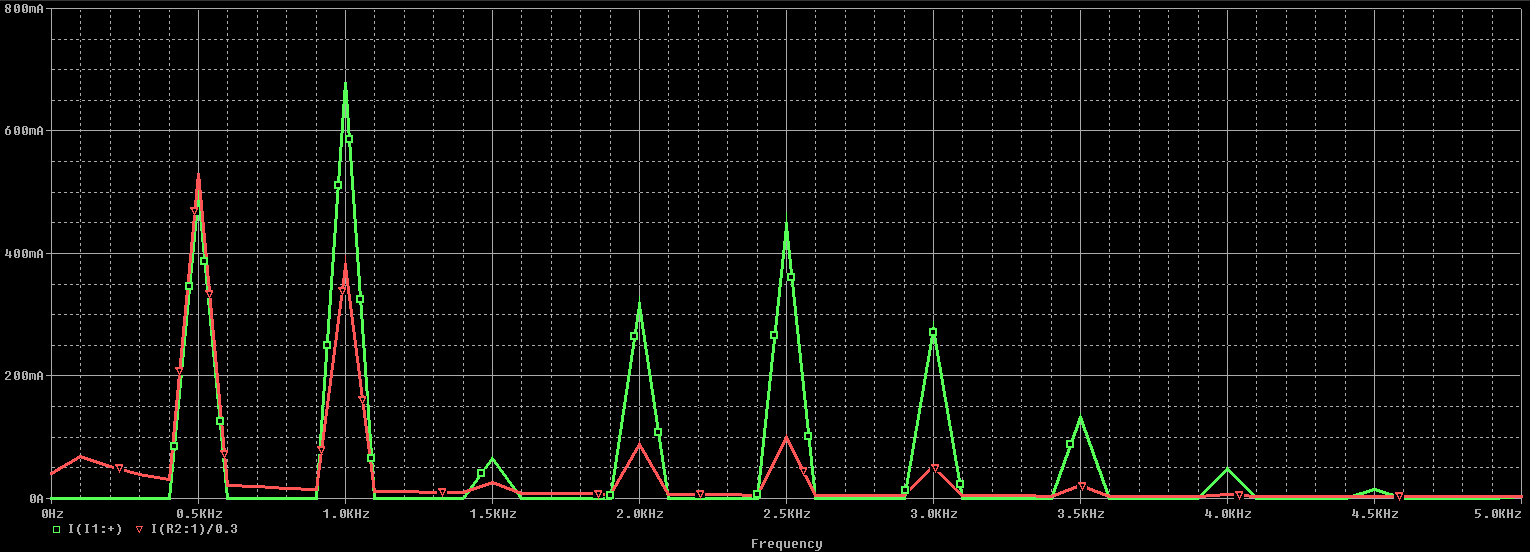
源波形（绿色）和负载波形（红色）中的频率内容。请注意，负载电流已通过最大值进行归一化，以提供更好的比较

注意，以上模拟是在阻性负载下进行的；频域中的唯一衰减是由于Pi网络引起的，而时域信号中的较大减小是由于负载电阻引起的。为了检查电抗性负载会发生什么，下面的示意图已用电感性负载L2代替了电阻性负载R2。

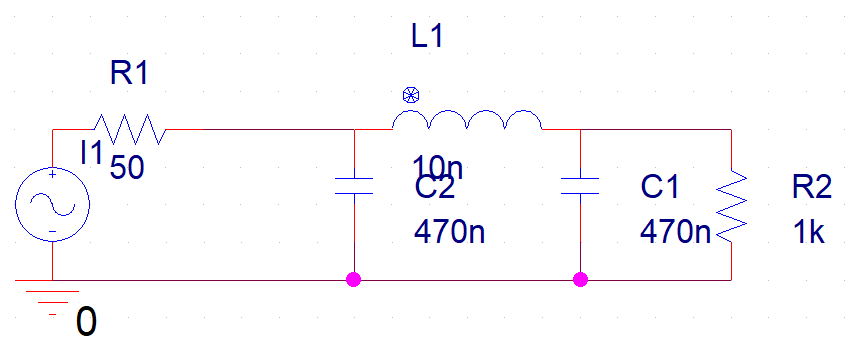
具有50 Ohm输出阻抗的FM源连接到Pi滤波器和下游负载（R2）

新负载具有高电感，在载波频率下的阻抗为62.83i欧姆，远低于原始的1000欧姆电阻。当我们再次运行仿真时，我们会看到截然不同的结果。下图显示了该新电路的时域源和负载结果。

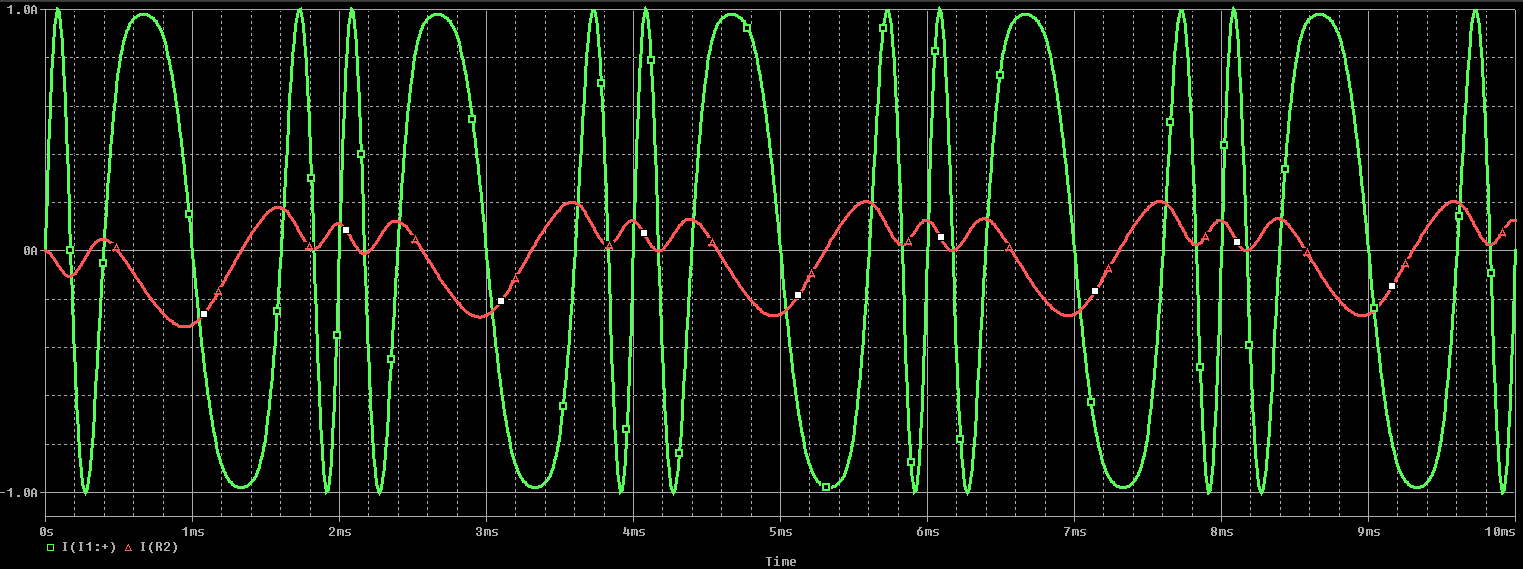
时域中源（绿色）和负载（红色）处的电流波形

在这里，由于电路中的总电阻较小，负载组件处的瞬态响应会很快消失（在〜0.1 ms之前）。在时域电流波形方面，我们看到在不同频率下会产生一些谐振。这可以从红色迹线（负载）与绿色迹线（源）的放大中看出。

在电路放大输入调制信号的地方可能并不明显。在这里，可以使用另一个傅里叶变换来提取每个信号中的频率内容，并在频谱图上进行比较。下图比较了每个信号的傅立叶变换。

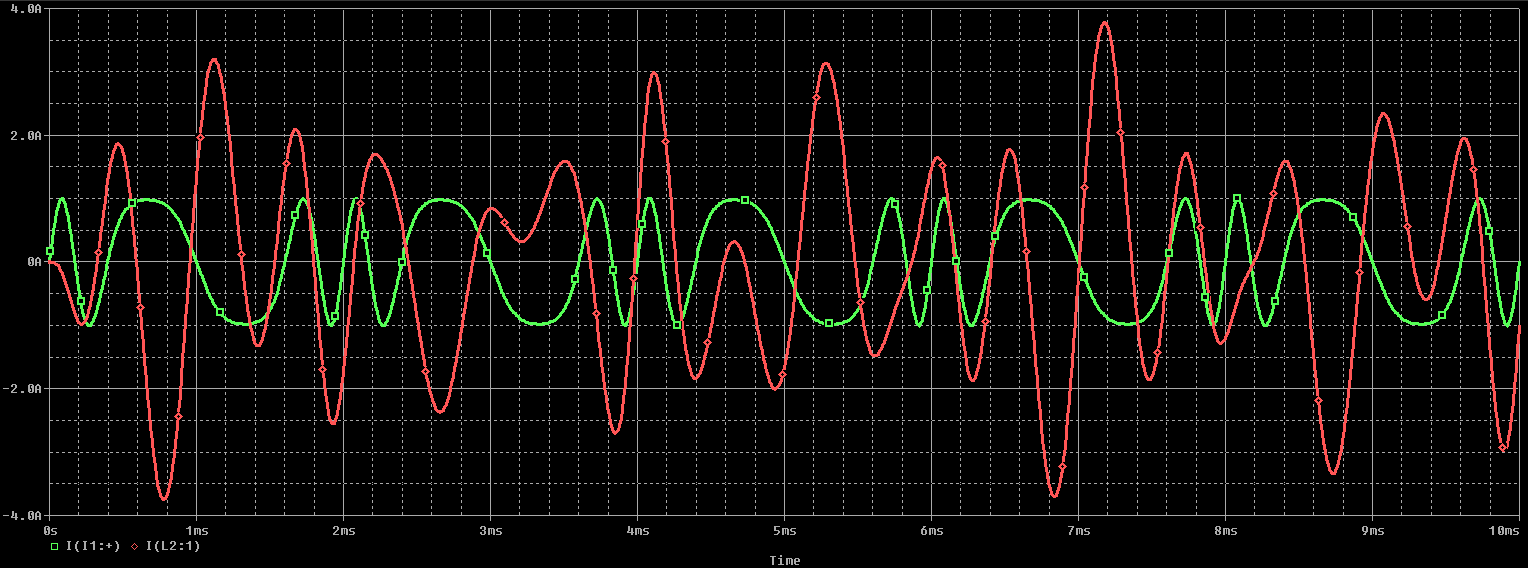
时域中源（绿色）和负载（红色）处的电流波形

从这里，我们可以看到在峰2-4中存在宽带放大，在峰3中放大明显。如果考虑此修改原理图中的布局，负载L2和输出电容器C1形成具有谐振的LC谐振电路频率为2.32 kHz。Pi滤波器中的其他组件会将这个谐振修改为较低的值，我们可以看到该谐振位于大约1.6 kHz。

超过〜2.5 kHz的滚降也稍大。可以预期这是由于以下事实：感性负载使Pi滤波器变成更复杂的4阶滤波器，因此衰减应该更大。这可以通过用扫频测量传递函数来研究。请注意，在负载位置连接和不连接L2的情况下都可以这样做，这将允许比较两个传递函数。

这应该表明负载组件的频率相关行为将如何影响电路中的上游组件以及负载所看到的结果信号。在电阻性负载的情况下，电路中的电阻会提供一定的衰减，而Pi滤波器会产生一些相移并使输入信号失真。当我们有感性负载时，电感会耦合回Pi滤波器，以创建更复杂的谐振频谱。